Stochastic Process Modeling

Modeling rare-event probabilities and performing hypothesis testing using Binomial, Poisson, and Gaussian distributions.

Python SciPy Hypothesis Testing Risk Analysis

Project Overview

In quantitative risk management, correctly modeling the probability of rare events (tail risk) is crucial. This project investigates the transition from Binomial distributions to Poisson and Gaussian limits, effectively modeling scenarios like default events or insurance claims.

The project also applies rigorous statistical hypothesis testing to determine if subpopulations deviate significantly from expected probability distributions, similar to detecting anomalies in market activity.

Key Concepts Implemented

Poisson Limit Theorem

Modeled low-probability events in large populations, demonstrating how Binomial variances converge to Poisson intensity rates.

Gaussian Approximation

Applied the Central Limit Theorem to approximate discrete distributions, enabling rapid analytically tractable risk bounds (VaR).

Statistical Hypothesis Testing

Calculated Z-scores and p-values to reject null hypotheses, a fundamental skill for backtesting trading strategies against random market noise.

Visual Analysis

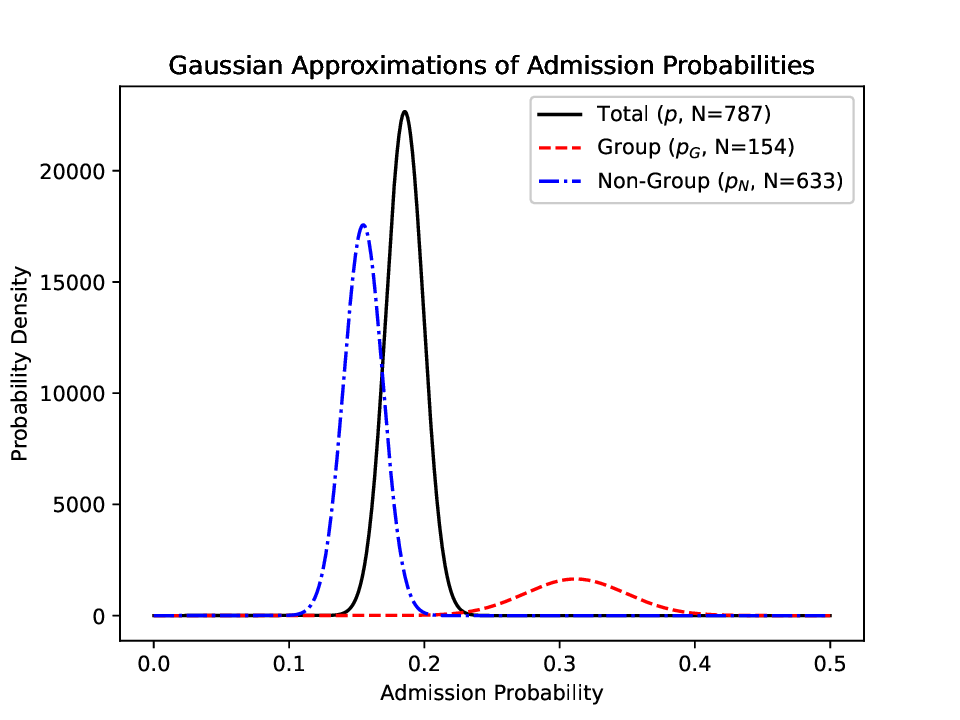
Gaussian Approximation Graph

Comparison of probability densities for different population subgroups, illustrating significant statistical deviations (anomalies) detected via Gaussian approximation.

Source Code

1. Hypothesis Testing (`p3_hw9.py`)

#!/usr/bin/env python3
import numpy as np
import matplotlib.pyplot as plt
from scipy import stats, special

N_total = 787
N_admit = 146

#Part a
p = N_admit / N_total
sigma_A = np.sqrt(N_total * p * (1 - p))
print(f"a. Standard deviation sigma_A: {sigma_A:.4f}")

#Part b
sigma_p =sigma_A / N_total
print(f"b. Uncertainty in p: {sigma_p:.4f}")

#Part c
N_sub = 154
k_cut = 48
prob_exact = np.sum(stats.binom.pmf(np.arange(k_cut, N_sub + 1), N_sub, p))
print(f"c. Exact probability (k >= 48): {prob_exact:.4e}")

#Part d
mu_sub = N_sub*p
sigma_sub = np.sqrt(N_sub*p*(1-p))
z = (k_cut-mu_sub)/(sigma_sub)
prob_gauss = 0.5*special.erfc(z / np.sqrt(2))
factor = prob_exact/prob_gauss
print(f"d. Gaussian approximation: {prob_gauss:.4e}")
print(f"Factor by Gaussian is small: {factor:.2f}")

#Part e
N_G = 154
N_AG = 48
p_G = N_AG / N_G
sigma_pG = np.sqrt(p_G * (1 - p_G) / N_G) 
print(f"e. p_G: {p_G:.4f}, Uncertainty: {sigma_pG:.4f}")

#Part f
N_rem = N_total-N_G
N_Arem = N_admit-N_AG
p_N = N_Arem/N_rem
sigma_pN = np.sqrt(p_N*(1-p_N) / N_rem)
print(f"f. p_N:{p_N:.4f},Uncertainty: {sigma_pN:.4f}")

#Part g
x = np.linspace(0, 0.5, 1000)

def get_y(x, mean, sigma, N):
    return (N / (sigma*np.sqrt(2* np.pi)))*np.exp(-0.5 * ((x - mean) / sigma)**2)

plt.plot(x, get_y(x, p, sigma_p, N_total), color='black', linestyle='solid', label=f'Total ($p$, N={N_total})')

plt.plot(x, get_y(x, p_G, sigma_pG, N_G), color='red', linestyle='dashed', label=f'Group ($p_G$, N={N_G})')

plt.plot(x, get_y(x, p_N, sigma_pN, N_rem), color='blue', linestyle='dashdot', label=f'Non-Group ($p_N$, N={N_rem})')

plt.xlabel('Admission Probability')
plt.ylabel('Probability Density')
plt.title('Gaussian Approximations of Admission Probabilities')
plt.legend()
plt.savefig('p3_hw9.eps')

2. Photon Counting Simulation (`p2_hw9.py`)

#!/usr/bin/env python3
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import poisson

# Part a
def simulate_photon_count():
    return np.random.binomial(1000, 0.002)

# Part b
counts = [simulate_photon_count() for _ in range(1000)]

# Part c
mu = 1000 * 0.002  
x = np.arange(0, np.max(counts) + 3)
y_poisson = 1000 * poisson.pmf(x, mu)

plt.figure()
plt.hist(counts, bins=np.arange(x.max() + 1) - 0.5, rwidth=0.8, label='Simulation')
plt.plot(x, y_poisson, color='red', marker='o', label=f'Poisson ($\mu={mu}$)')
plt.title('Photon Counting Simulation (1000 Trials)')
plt.xlabel('Number of Photons Detected')
plt.ylabel('Frequency')
plt.legend()
plt.savefig('p2_hw9.eps')
Back to Projects