Numerical PDE Solver (Finite Difference)

Solving Partial Differential Equations using the Relaxation Method on a discretised 2D grid, applicable to Heat Equations and Black-Scholes models.

Python Finite Difference Method Numerical Analysis PDEs

Project Overview

Partial Differential Equations (PDEs) govern heat diffusion, fluid dynamics, and option pricing in finance (Black-Scholes). This project implements a numerical solver from scratch using the Finite Difference Method to solve Laplace's equation ($\nabla^2 V = 0$) and other boundary value problems.

The implementation uses the "Relaxation Method," an iterative process that converges to the steady-state solution, demonstrating core concepts used in industry-grade PDE solvers for derivative pricing.

Key Concepts Implemented

Finite Difference Method

Discretized continuous derivatives into difference equations on a grid, converting calculus problems into matrix algebra manageable by computers.

Relaxation Algorithm

Implemented an iterative averaging algorithm where each grid point is updated based on its neighbors, simulating the physical process of diffusion.

Boundary Conditions

Handled Dirichlet boundary conditions (fixed values at edges) which equate to boundary options or fixed-rate constraints in financial models.

Visual Analysis

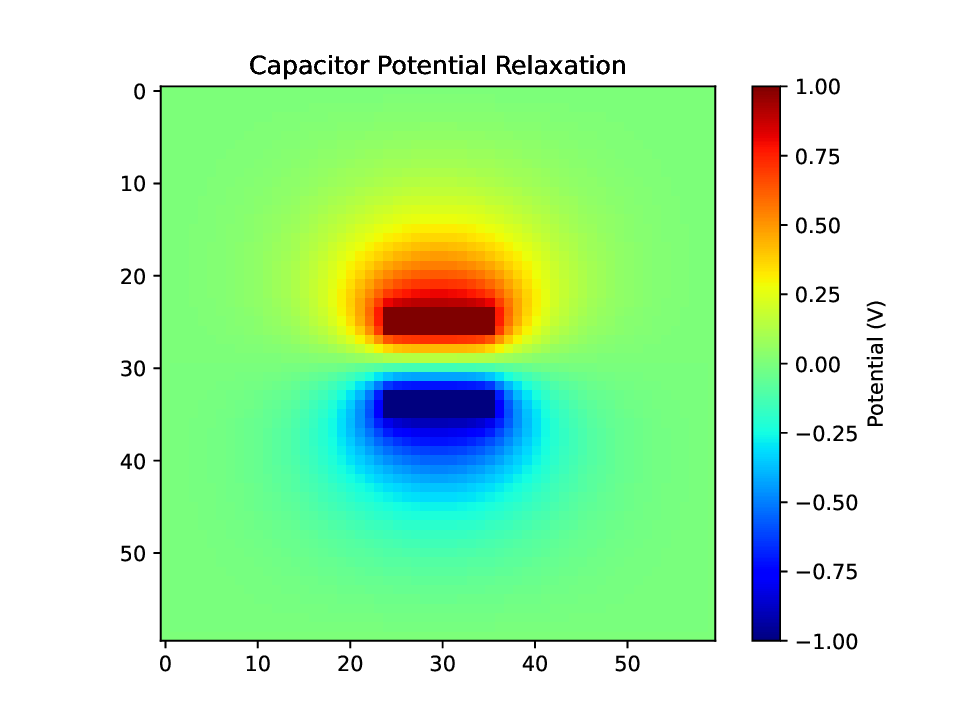
Potential Field Heatmap

Heatmap visualization of the electric potential field relaxing to a steady state between two capacitor plates. The color gradient represents the potential magnitude.

Source Code: PDE Solver (`p1_hw10.py`)

#!/usr/bin/env python3
#First eps file is 256 iterations, gridsize 60, plate thickness 0.05,plate
#width 0.2, gap between plates being 2*plate thickness which is 0.1, and voltage
#equal to 1.
#The second file is 100000 iterations (as I wanted to see if the converging num
#ber changes).
#The last file is the "dipole", as I changed the gap between plates being 10*plate thickness.


import numpy as np
import matplotlib.pyplot as plt
import time

ITER = 256
#ITER=100000
GRIDSIZE = 60
PTH = 0.05
PWID = 0.2
GAP = 2.0 * PTH
#GAP = 10.0 * PTH
VOLTAGE = 1.0

def load_boundary(darray, gridsize):
    """Place predetermined potential at boundary points."""
    clx = int(0.5 * gridsize * (1.0 - PWID))
    cux = gridsize - clx
    capth = (2.0 * PTH + GAP) * gridsize
    cly1 = int(0.5 * (gridsize - capth))
    cuy1 = int(cly1 + gridsize * PTH)
    cly2 = int(cly1 + gridsize * (GAP + PTH))
    cuy2 = gridsize - cly1
    darray[clx:cux, cly1:cuy1] = -VOLTAGE
    darray[clx:cux, cly2:cuy2] = VOLTAGE
    darray[0, :] = 0.0        
    darray[gridsize-1, :] = 0.0 
    darray[:, 0] = 0.0  
    darray[:, gridsize-1] = 0.0

olddata = np.zeros((GRIDSIZE, GRIDSIZE))
newdata = np.zeros((GRIDSIZE, GRIDSIZE))
load_boundary(olddata, GRIDSIZE)

print(f"Starting simulation with {ITER} iterations on grid {GRIDSIZE}x{GRIDSIZE}...")

t0 = time.perf_counter()

for i in range(ITER):
    newdata = 0.25 * (np.roll(olddata, 1, axis=0) + 
                      np.roll(olddata, -1, axis=0) + 
                      np.roll(olddata, 1, axis=1) + 
                      np.roll(olddata, -1, axis=1))
    load_boundary(newdata, GRIDSIZE)
    diff = np.abs(newdata - olddata).sum()
    print('iteration: %d difference sum: %.16f' % (i, diff))
    olddata = np.copy(newdata)

elapsed = time.perf_counter() - t0
print()
print('Time elapsed: %.6f s' % elapsed)

# Plotting
plotarr = np.flipud(olddata.transpose(1, 0))
fig, ax = plt.subplots(dpi=180)
im = ax.imshow(plotarr, interpolation='none', cmap='jet')
plt.colorbar(im, label='Potential (V)')
plt.title("Capacitor Potential Relaxation")
output_filename='capacitor_config_1.eps'
plt.savefig(output_filename,format='eps')
plt.show()

input("\nPress  to exit . . . \n")
Back to Projects