Monte Carlo Methods & Stochastic Calculus

Solving deterministic problems through random sampling, with applications in options pricing and risk assessment.

Python NumPy Stochastic Calculus Financial Modeling

Project Overview

This project explores the power of Monte Carlo simulations to solve complex deterministic problems where analytical solutions are difficult or impossible. By leveraging the Law of Large Numbers, the simulation converges to the true value with an error rate scaling as $1/\sqrt{N}$.

In quantitative finance, these methods are the standard for pricing complex derivatives (like Asian or Lookback options) where the path-dependency makes standard Black-Scholes formulas inapplicable.

Key Concepts Implemented

Convergence Analysis

Verified the $O(N^{-1/2})$ convergence rate of Monte Carlo integration. This theoretical foundation is critical for estimating computation costs in high-frequency trading simulations.

Stochastic Integration

Implemented numerical integration techniques utilizing random sampling to approximate high-dimensional integrals, a common problem in risk model calibration.

Variance Reduction

Analyzed error metrics to understand stability and precision of the estimates, precursors to implementing variance reduction techniques like Antithetic Variates.

Visual Analysis

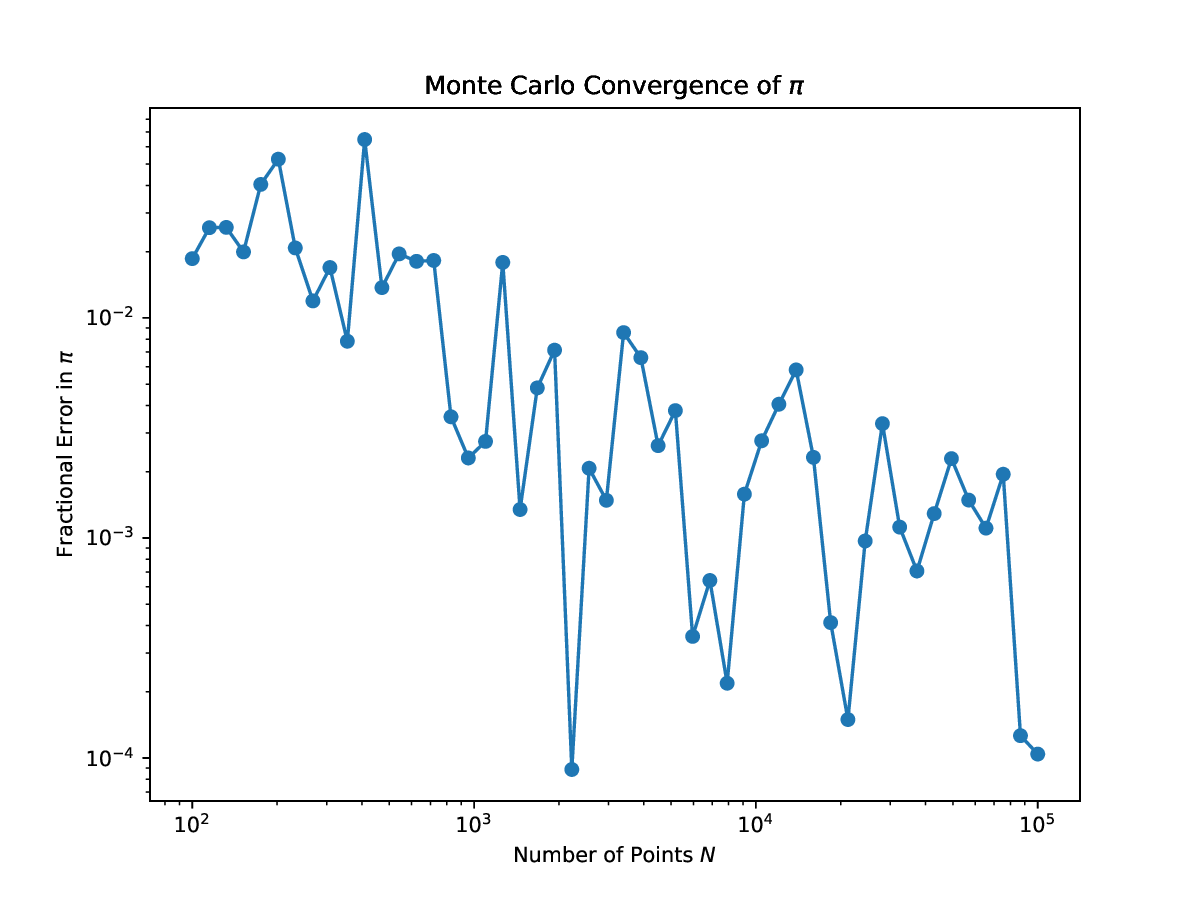
Monte Carlo Convergence Graph

Log-log plot showing the fractional error in estimating $\pi$ decreasing as the number of samples increases, confirming the $1/\sqrt{N}$ convergence rate.

Source Code

1. Monte Carlo Integration vs Riemann Sum (`p4_hw9.py`)

#!/usr/bin/env python3
import numpy as np
import matplotlib.pyplot as plt


KNOWN_VALUE = np.sqrt(np.pi)
LIMIT = 10.0  

def riemann_sum(N):
    dx = (2 * LIMIT) / N
    x_rect = np.linspace(-LIMIT, LIMIT - dx, N)
    y_rect = np.exp(-x_rect**2)
    return dx * np.sum(y_rect)

def monte_carlo_simulation(N):
    x_mc = np.random.uniform(-LIMIT, LIMIT, N)
    return (2 * LIMIT) * np.mean(np.exp(-x_mc**2))

def main():
    N_values = np.logspace(1, 6, 20, dtype=int)
    rect_errors = []
    mc_errors = []
    for N in N_values:
        #part a
        rect_val = riemann_sum(N)
        r_err = (rect_val - KNOWN_VALUE) / KNOWN_VALUE
        rect_errors.append(abs(r_err))

        #part b
        mc_val = monte_carlo_simulation(N)
        m_err = (mc_val - KNOWN_VALUE) / KNOWN_VALUE
        mc_errors.append(abs(m_err))

    #part a
    plt.loglog(N_values, rect_errors, 
               color='blue', linestyle='none', marker='o', 
               label='Rectangle Method (Left Sum)')
    
    plt.xlabel('Number of Rectangles (N)')
    plt.ylabel('Fractional Error (Absolute)')
    plt.title(r'Riemann Sum Error for $\int e^{-x^2} dx$')
    plt.legend()
    plt.savefig('p4_hw9_integration.eps')
    plt.close()

    #part b
    plt.loglog(N_values, mc_errors, 
               color='red', linestyle='none', marker='s', 
               label='Monte Carlo Simulation')

    plt.xlabel('Number of Random Points (N)')
    plt.ylabel('Fractional Error (Absolute)')
    plt.title(r'Monte Carlo Error for $\int e^{-x^2} dx$')
    plt.legend()
    plt.savefig('p4_hw9_monte_carlo.eps')
    plt.close()

if __name__ == "__main__":
    main()

2. Pi Estimation Convergence (`Monte_Carlo_Convergence_of_pi.py`)

#!/usr/bin/env python3
import numpy as np
import matplotlib.pyplot as plt

N_min=100
N_max=100000

N_values = np.geomspace(N_min, N_max, num=50, dtype=int) #I can also use np.logspace but found out that np.geomspace is better
fractional_errors = []

for N in N_values:
    points = np.random.uniform(0, 2, (N, 2))
    dist_sq = np.sum((points- 1)**2, axis=1)
    pi_est = 4 * np.mean(dist_sq <= 1)
    error = np.abs(pi_est-np.pi) /np.pi
    fractional_errors.append(error)

plt.figure(figsize=(8, 6))
plt.plot(N_values, fractional_errors, 'o-')
plt.xscale('log') 
plt.yscale('log')
plt.xlabel('Number of Points $N$')
plt.ylabel('Fractional Error in $\pi$')
plt.title('Monte Carlo Convergence of $\pi$')
plt.savefig('Monte_Carlo_Convergence_of_pi.eps', format='eps')
plt.show()
Back to Projects